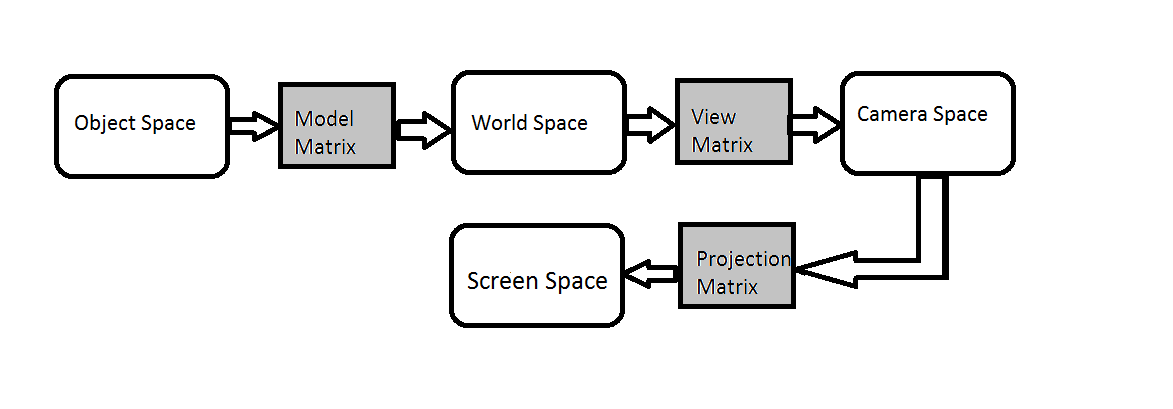
To get a 3d model visible on a screen, all of its vertices needs to be transformed through 4-graphic spaces, these are as follows.
Objects space
Objects are created in its own co-ordinate system and position of object vertices are defined with respect to, its Object space.
World space
All objects are transformed into world space.
All operations of object movement are done in this space and then projection of this space is visible on screen based on camera position.
Transformation of objects from object space to word space is done using the matrix operations on the vertices of the object, this matrix is called Model matrix.
Every object has its own Model matrix.
Camera space
Eye space or camera is a transformed view of our objects from the camera location.
There is a matrix to transform the objects into eye space or camera space.
This matrix is called View matrix.
Although in ThreeJS there is one matrix to do the world and View transformation and it's called modelView matrix.
Screen space or Projection
This is a projection of Camera space into a 2D co-ordinate system and matrix to transform this is known as Projection matrix.
So to transform a vertex from the object space position(xyz) to screen space, we need to multiply it with modelViewMatrix and projectionMatrix.
Screen position = projectionMatrix * modelViewMatrix * Oposition(xyz)
0 Comment(s)